功能经典例题
在第24届冬季奥林匹克运动会上,某运动员在进行跳台滑雪比赛的时候,从跳台边缘的0点以某一速度水平滑出。如图所示,A、B、C为其运动轨迹上的三个点,且AB连线与BC连线在水平方向上的投影相等,忽略空气阻力,关于运动员在AB段与BC连线在水平方向投影相等,忽略空气阻力,关于空气阻力,关于运动员在AB段与BC段的运动,下列说法正确的是
A、速度的变化量相同
B、速率的变化量相同
C、动能的变化量相同
D、动能的变化量相同
展开答案
【答案】A
【解析】AB、BC水平距离一样,时间一样,则竖直方向的$\Delta v=gt$ ,A对
用铁锤把小铁钉钉入木板,设木板对钉子的阻力与钉进木板的深度成正比,已知铁锤第一次将钉子钉进d,如果铁锤第二次敲钉子时对钉子做的功与第一次相同,那么,第二次钉子进入木板的深度是( )
A、$(\sqrt{3}-1)d$ B、$(\sqrt{2}-1)d$ C、$\dfrac{\sqrt{51}}{2}d$ D、$\dfrac{\sqrt{2}}{2}d$
展开答案
高中生一旦学到功和能就会掉队,因为缺少对整体的理解。主要是能量守恒,动量守恒,力的平衡,运动的等量关系。复习时候要多思考这些,才会事半功倍,在实际生活中,这也是不可或缺的技能。
假设摩擦系数是k,那么第一次做功就是
$W_1=FS=kd \times d=\dfrac{1}{2}kd^2$
假设第二次最终距离是x
$W_2=FS=kx \times x=\dfrac{1}{2}kx^2$
第二次敲钉子时对钉子做的功与第一次相同
所以$2w_1=w_2$
可以很轻松的得到$x=\sqrt{2}d$
第二次钉子进入木板的深度是$(\sqrt{2}-1)d$
将一个小球从地面竖直上抛,此过程中小球受到的空气阻力与速率成正比,设向上为正方向,小球的速度、位移、动能和机械能分别为v、x、$E_k$和E,以地面为零势能面,则下列描述小球运动过程的图像可能正确的是( )
展开答案
答案【C】
解析:这类题一般是先要画图了解过程,然后受力分析,然后写出表达式,如果不能写出也要能定性分析。
小球上抛过程$mg+kv=ma$,加速度逐渐减小。
小球下落过程$mg-kv=ma$,加速度逐渐减小
但是速度为0的时候,加速度不为零,斜率不是0,所以A错。
速度位移关系一样写出一个表达式
上抛过程 $\dfrac{1}{2}mv^2=\dfrac{1}{2}v_0^2-(mg+kv)x$ 解得:$v^2=v_0^2-2(g+\dfrac{kv}{m})$速度随着斜率减小
下落过程 $\dfrac{1}{2}mv^2=(mg-kv)x$ 解得:$v^2=2(g-\dfrac{kv}{m})$,随着速度增加斜率减小.所以B错
关于动能
上抛$E_K=E_{K0}-(mg+kv)x$,斜率逐渐减小
下落$E_K=(mg-kv)x$,斜率逐渐减小 所以C对!
关于能量
上抛$E=E_0-kvx$,速度减小,斜率减小。
下落$E=E_0′-kv’x$ ,速度增大,斜率增大。
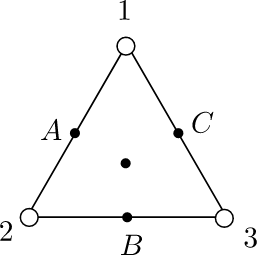
如图所示,光滑绝缘水平面上,有1、2、3三个带电量均为十g、质量均为m的相同金属小球,用长为L的三根绝缘细绳连接着,A、B、C分别为其中点,O点为三角形的中心,已知单个点电荷q周围空间的电势为$\varphi=k\dfrac{q}{r}$,r为到点电荷的距离,则下列说法正确的是
A.O点的电场强度不为零,且方向向上
B.若L长度可调节,则A、O两点的电势可能相等
C.系统的总电势能为$E_p=k\dfrac{2q^2}{L}$
D.若将B处剪断,则之后小球1的最大速度为$v_{1m}=q\sqrt{\dfrac{2k}{3mL}}$
展开答案
【答案】D
【解析】势能本身就是力被限制产生的,也就是说从当前位置移动到无穷远处或者到0电势面所做的功,就是当前势能。
ABC在O点产生的合力为0,那么这个地方电场强度也是0,那么该点的电势能也是0.A错
A点的电势$\varphi_A=2k\dfrac{q}{\dfrac{L}{2}}+k\dfrac{q}{\dfrac{\sqrt{3}L}{2}}$
O点的电势$\varphi_o=3k\dfrac{q}{\dfrac{L}{\sqrt{3}}}$
很明显二者不同 B错
1处小球的电势能为$E_{p1}=\varphi q=q(\varphi_2+\varphi_3)=2k\dfrac{q^2}{L}$
$E_{p1}=$E_{p2}=$E_{p3}$,系统的总电势能$E_{p}=\dfrac{E_{p1}=E_{p2}=E_{p3}}{2}=3k\dfrac{q^2}{L}$ :C错误
若将B剪段,则1在AC方向上速度为0,在OB方向三动量守恒$0=mv_1-2mv_2$
三个小球运动在一条直线的时候电势能最小,电势能最小时,动能最大!
此时1的电势能$E_{p1}=2k\dfrac{q^2}{L}$ ,23的电势能$E_{p1}=E_{p2}=\dfrac{3kq^2}{2L}$
此时电势能大小为$E_p=k\dfrac{5q^2}{2L}$
$3k\dfrac{q^2}{L}-k\dfrac{5q^2}{2L}=\dfrac{1}{2}mv_1^2+\dfrac{1}{2} \times 2m v_2^2$
解得$v_{1m}=q\sqrt{\dfrac{2k}{3mL}}$
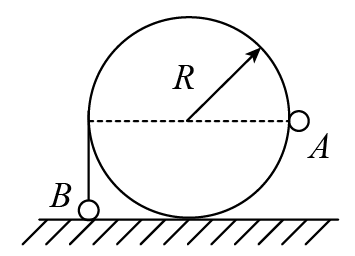
如图,可视为质点的小球A、B用不可伸长的细软轻线连接,跨过固定在地面上、半径为R的光滑圆柱,A的质量为B的两倍.当B位于地面时,A恰与圆柱轴心等高.将A由静止释放,B上升的最大高度是 ( )
A.2R B.5R/3
C.4R/3 D.2R/3
展开答案
【答案】C
C
【解析】当A下落至地面时,B恰好上升到与圆心等高位置,这个过程中机械能守恒,
即:$2mgR-mgR=\dfrac{1}{2}3mv^2$
接下来,B物体做竖直上抛运动,再上升的高度$h=\dfrac{v^2}{2g}$
两式联立得$h=\dfrac{R}{3}$
这样B上升的最大高度H=h+R=4R/3
(2015·北京·高考真题)“蹦极”运动中,长弹性绳的一端固定,另一端绑在人身上,人从几十米高处跳下.将蹦极过程简化为人沿竖直方向的运动.从绳恰好伸直,到人第一次下降至最低点的过程中,下列分析正确的是()
A.绳对人的冲量始终向上,人的动量先增大后减小
B.绳对人的拉力始终做负功,人的动能一直减小
C.绳恰好伸直时,绳的弹性势能为零,人的动能最大
D.人在最低点时,绳对人的拉力等于人所受的重力
展开答案
【答案】A
【解析】A.由于绳对人的作用力一直向上,故绳对人的冲量始终向上;由于人在下降中速度先增大后减小,动量先增大后减小;故A正确;
B.在该过程中,拉力与运动方向始终相反,绳子的力一直做负功;但由分析可知,人的动能先增大后减小;故B错误;
C.绳子恰好伸直时,绳子的形变量为零,弹性势能为零;但此时人的动能不是最大,故C误;
D.人在最低点时,绳子对人的拉力一定大于人受到的重力;故D错误.
(2015·江苏·高考真题)(多选)如图所示,轻质弹簧一端固定,另一端与质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h.圆环在C处获得一竖直向上的速度v,恰好能回到A;弹簧始终在弹性限度之内,重力加速度为g,则圆环( )
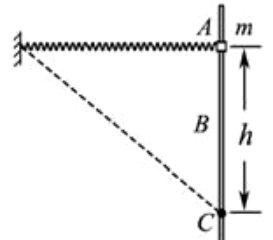
A.下滑过程中,加速度一直减小
B.下滑过程中,克服摩擦力做功为$\dfrac{1}{4}mv^2$
C.在C处,弹簧的弹性势能为$\dfrac{1}{4}mv^2-mgh$
D.上滑经过B的速度大于下滑经过B的速度
展开答案
由题意知,圆环从 A 到 C 先加速后减速,到达 B 处的加速度减小为零,故加速度先减小后增大,故 A 错误;从 A 到 C,
根据能量守恒: \[ mgh = W_{f}+E_{p} \]
从 C 到 A: \[ \frac{1}{2}mv^{2}+E_{p}=mgh + W_{f} \]
联立解得: \[ W_{f}=\frac{1}{4}mv^{2},E_{p}=mgh – \frac{1}{4}mv^{2} \] 所以 B 正确,C 错误;
从 A 到 B: \[ mgh_{1}=\frac{1}{2}mv_{B1}^{2}+\Delta E_{p1}+W_{f1} \]
从 C 到 A: \[ \frac{1}{2}mv^{2}+\Delta E_{p2}=\frac{1}{2}mv_{B2}^{2}+W_{f2}+mgh_{2}
\frac{1}{2}mv^{2}+E_{p}=mgh + W_{f} \]
联立可得 \( v_{B2}>v_{B1} \),所以 D 正确。
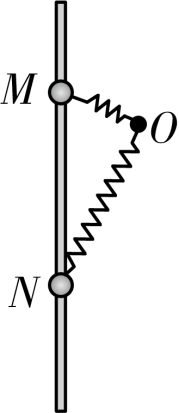
(2016·全国·高考真题)(多选)如图,小球套在光滑的竖直杆上,轻弹簧一端固定于O点,另一端与小球相连.现将小球从M点由静止释放,它在下降的过程中经过了N点.已知M、N两点处,弹簧对小球的弹力大小相等,且∠ONM<∠OMN<$\dfrac{\pi}{2}$.在小球从M点运动到N点的过程中
A.弹力对小球先做正功后做负功
B.有两个时刻小球的加速度等于重力加速度
C.弹簧长度最短时,弹力对小球做功的功率为零
D.小球到达N点时的动能等于其在M、N两点的重力势能差
展开答案
【答案】BCD
BCD
【解析】A.因M和N两点处弹簧对小球的弹力大小相等,且∠ONM<∠OMN<知M处的弹簧处于压缩状态,N处的弹簧处于伸长状态,则弹簧的弹力对小球选做负功后正功,选项A错误.
B.当弹簧水平时,竖直方向的力只有重力,加速度为g;当竖直方向的合外力为mg时,加速度为也g,则有两个时刻的加速度大小等于g,选项B正确;
C.弹簧长度最短时,即弹簧水平,弹力与速度垂直,则做功的功率为零,选项C正确;
D.由M→N的动能定理$W_{FK}+W_G=\Delta E_K$,因M和N两点处弹簧对小球的弹力大小相等,则由弹力作功特点知$W_{FK}=0$,即$W_{G}=\Delta E_K$,选项D正确.
(2013·安徽·高考真题)质量为m的人造地球卫星与地心的距离为r时,引力势能可表示为$E_P=-\dfrac{GMm}{r}$,其中 G为引力常量,M为地球质量。该卫星原来的在半径为R1的轨道上绕地球做匀速圆周运动,由于受到极稀薄空气的摩擦作用,飞行一段时间后其圆周运动的半径变为R2,此过程中因摩擦而产生的热量为( )
A. $GMm(\frac{1}{R_{2}} – \frac{1}{R_{1}})$
B.$GMm(\frac{1}{R_{1}} – \frac{1}{R_{2}})$
C.$\frac{GMm}{2}(\frac{1}{R_{2}} – \frac{1}{R_{1}})$
D.$\frac{GMm}{2}(\frac{1}{R_{1}} – \frac{1}{R_{2}})$
展开答案
C 【解析】卫星做匀速圆周运动,万有引力提供向心力 \[ \frac{GMm}{r^{2}} = m\frac{v^{2}}{r} \] 可得质量为 \(m\) 的人造地球卫星与地心的距离为 \(r\) 时的动能为 \[ E_{k} = \frac{1}{2}mv^{2} = \frac{GMm}{2r} \] 结合题意,此时卫星的机械能 \(E = E_{k} + E_{p} = -\frac{GMm}{2r}\) 根据能量守恒定律,该卫星因摩擦而产生的热量等于卫星损失的机械能,所以 \[ Q = E_{1} – E_{2} = -\frac{GMm}{2R_{1}} – (-\frac{GMm}{2R_{2}}) = \frac{GMm}{2}(\frac{1}{R_{2}} – \frac{1}{R_{1}}) \] ,故选 C。
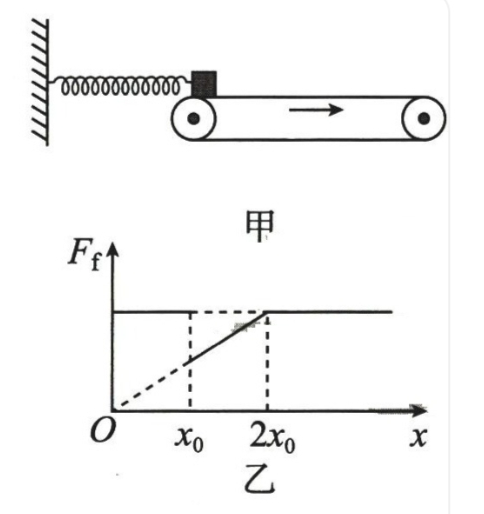
7. 如图甲所示,足够长的水平传送带以某一恒定速率顺时针转动,一根轻弹簧两端分别与物块和竖直墙面连接,将物块在传送带左端无初速度释放,此时弹簧恰处于原长且为水平。物块向右运动的过程中,受到的摩擦力大小与物块位移的关系如图乙所示。已知物块质量为\(m\),物块与传送带间的动摩擦因数为\(\mu\),重力加速度为\(g\),最大静摩擦力等于滑动摩擦力,\(x_{0}\)为已知量,则 ( )
A. \(0 ~ x_{0}\)过程,物块所受的摩擦力方向向左
B. \(x_{0} ~ 2x_{0}\)过程,物块做匀加速运动
C. 弹簧的劲度系数为\(\frac{\mu mg}{2x_{0}}\)
D. 传送带的速度为\(\sqrt{\frac{3\mu gx_{0}}{4}}\)
展开答案
【C】
物块在刚释放的一段时间内相对传送带向左滑动,受到向右的滑动摩擦力,同时弹簧弹力逐渐增大,由题图乙可知当\(x = x_{0}\)时,摩擦力发生突变,瞬间减小后,随着\(x\)正比例增大,考虑到弹簧弹力也是随\(x\)成正比例增大,由此可推知当\(x = x_{0}\)时,物块刚好与传送带达到共同速度,之后随着传送带继续向右运动,在\(x ~ 2x_{0}\)过程物块始终相对传送带静止,弹力和静摩擦力同时增大且平衡,物块做匀速直线运动,当\(x = 2x_{0}\)时,弹簧弹力大小增大至与滑动摩擦力大小相同,\(AB\)错误;根据前面分析可知,弹簧的劲度系数为\(k = \frac{\mu mg}{2x_{0}}\),\(C\)正确;
在\(0 ~ x_{0}\)过程,弹簧弹力从零线性增大到\(kx_{0}\),则此过程的平均弹力大小为\(\overline{F}_{\text{T}}=\frac{0 + kx_{0}}{2}=\frac{\mu mg}{4}\),设传送带的速度为\(v\),此过程对物块根据动能定理有\(\frac{1}{2}mv^{2}=\mu mgx_{0}-\overline{F}_{\text{T}}x_{0}\),解得\(v = \sqrt{\frac{3\mu gx_{0}}{2}}\),\(D\)错误。
(2009·江苏·高考真题)(多选)如图所示,两质量相等的物块A、B通过一轻质弹簧连接,B足够长、放置在水平面上,所有接触面均光滑。弹簧开始时处于原长,运动过程中始终处在弹性限度内。在物块A上施加一个水平恒力,A、B从静止开始运动到第一次速度相等的过程中,下列说法中正确的有( )
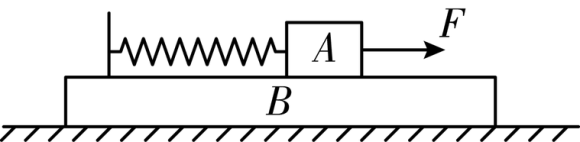
A.当A、B加速度相等时,系统的机械能最大
B.当A、B加速度相等时,A、B的速度差最大
C.当A、B的速度相等时,A的速度达到最大
D.当A、B的速度相等时,弹簧的弹性势能最大
展开答案
答案:BCD
解析:
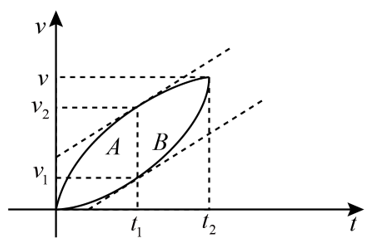
(2022·江西赣州·一模)(多选)如图甲所示,质量为m=0.1kg的滑块(可视为质点),在内壁光滑、固定的水平筒内压缩弹簧,弹簧原长小于筒长,且弹簧与滑块不拴接。滑块由静止释放,离开筒后立即滑上位于水平面上的木板左端,此后木板的速度-时间图象如图乙所示,已知木板质量M=0.2kg,最终滑块恰好没有离开木板,重力加速度g取10m/s2,则( )
A.滑块与木板之间的动摩擦因数为0.1
B.木板长度为0.75m
C.释放滑块时弹簧的弹性势能为0.45J
D.木板与水平面间因摩擦产生的热量为0.375J
展开答案
【答案】BC
【解析】A. 设木板与地面之间的摩擦因数为\(\mu_{2}\),木板做匀减速的加速度为\(a_{3}\),根据牛顿第二定律得 \(\mu_{2}(M + m)g = (M + m)a_{3}\) 根据图像得
\(a_{3} = \frac{0.5}{1.0 – 0.5}m/s^{2} = 1m/s^{2}\)解得\(\mu_{2} = 0.1\)
设滑块与木板之间的摩擦因数为\(\mu_{1}\),木板做匀加速的加速度为\(a_{2}\),根据牛顿第二定律得 \(\mu_{1}mg – \mu_{2}(M + m)g = Ma_{2}\)
根据图像得\(a_{2} = \frac{0.5}{0.5}m/s^{2} = 1m/s^{2}\) 解得\(\mu_{1} = 0.5\) 滑块与木板之间的动摩擦因数为\(0.5\),
A错误; B. 设滑块的加速度为\(a_{1}\),根据牛顿第二定律得\(\mu_{1}mg = ma_{1}\)
解得\(a_{1} = 5m/s^{2}\) 根据逆向思维,滑块滑上木板时的速度为\(v_{0} = 0.5 + a_{1}×0.5 = 3m/s\) 木板长度为\(L = \frac{3 + 0.5}{2}×0.5m – \frac{0.5×0.5}{2}m = 0.75m\) ,B正确;
C. 根据机械能守恒定律得,释放滑块时弹簧的弹性势能为\(E_{p} = \frac{1}{2}mv_{0}^{2} = 0.45J\) ,C正确;
D. 木板与水平面间因摩擦产生的热量为\(Q = \mu_{2}(M + m)g×\frac{1×0.5}{2} = 0.075J\) ,D错误。故选BC。
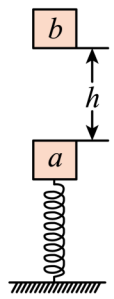
(2022·山东·模拟预测)(多选)如图所示,一竖直轻质弹簧下端固定在水平地面上,上端与质量为\(m\)的物块\(a\)连接,初始时\(a\)保持静止。现有一质量为\(m\)的物块\(b\)从距\(a\)正上方\(h\)处自由释放,与\(a\)发生碰撞后一起运动但不粘连,压缩弹簧至最低点,然后一起上升到最高点时物块\(b\)恰好不离开物块\(a\)。物块\(a\)、\(b\)均可视为质点,弹簧始终处于弹性限度内,其弹性势能\(E_{\text{p}}=\frac{1}{2}kx^{2}\)(\(k\)为弹簧的劲度系数,\(x\)为弹簧的形变量),重力加速度为\(g\),下列说法正确的是( )
A. 两物块由于碰撞损失的机械能为\(\frac{mgh}{3}\)
B. 从碰撞后到最高点,整个系统弹性势能的减少量为\(\frac{mgh}{6}\)
C. 从碰撞后到最高点,两物块的最大动能为\(\frac{2mgh}{3}\)
D. 整个系统弹性势能的最大值为\(\frac{8mgh}{3}\)
展开答案
【BCD】
【解析】A.质量为\(m\)的物块\(b\)从距\(a\)正上方\(h\)处自由释放,根据机械能守恒,可得到达物体\(a\)时\(b\)的速度为\(mgh = \frac{1}{2}mv^{2}\) 解得\(v = \sqrt{2gh}\) \(A\)与\(b\)碰撞的过程中,动量守恒,则有\(mv = 2mv_{\text{共}}\) 两物块由于碰撞损失的机械能为\(\Delta E=\frac{1}{2}mv^{2}-\frac{1}{2}\cdot 2mv_{\text{共}}^{2}=\frac{1}{2}mgh\),\(A\)错误; \(B\).
一起上升到最高点时物块\(b\)恰好不离开物块\(a\),则此时弹簧处在原长位置,设此时物体上升的高度为\(h_{1}\),则有 \(\frac{1}{2}\cdot 2m\cdot v_{\text{共}}^{2}+\frac{1}{2}kh_{1}^{2}=2m\cdot gh_{1}\)
又\(kh_{1}=mg\)
解得\(h_{1}=\frac{1}{3}h\) 从碰撞后到最高点,整个系统弹性势能的减少量为
\(\frac{1}{2}\cdot 2m\cdot v_{\text{共}}^{2}-\frac{1}{2}\cdot 2m\cdot g\cdot \frac{1}{3}h=\frac{1}{6}mgh\),\(B\)正确;
\(C\).当弹簧的弹力大小与两物块的重力大小相等时,此时有两物块的最大动能 \(E_{km}=\frac{1}{2}\cdot 2m\cdot v_{\text{共}}^{2}+\frac{1}{6}mgh=\frac{2}{3}mgh\),\(C\)正确;
\(D\).当两物体的速度减为零时,整个系统弹性势能取得最大值,此时最大值为 \(E_{pm}=E_{km}+E_{\text{p}}=\frac{8mgh}{3}\),\(D\)正确。故选\(BCD\)。
如图甲为海盗桶玩具,当插进桶内的剑触发桶内开关时,小海盗就从木桶顶部突然跳出来。其原理可简化为图乙所示,弹簧压缩后被锁扣K锁住,打开锁扣K,小球被弹射出去,A位置为弹簧原长,忽略弹簧质量和空气阻力,小球从B到A的过程中,下列说法正确的是( )
甲图为海盗桶玩具实物图,乙图为原理简化图,图中有一个容器,容器内有弹簧,弹簧上方有小球,小球所在位置标为B,容器上方有一虚线位置标为A,小球右侧有锁扣K。
A. 小球的机械能守恒
B. 小球的速度一直在增大
C. 小球的加速度先增大后减小
D. 小球与弹簧组成的系统重力势能与弹性势能之和先减小后增大
展开答案
答案:D
机械能守恒定律+牛顿第二定律 小球从B到A过程中,弹簧弹力对小球做正功,小球的机械能增加,A错误;弹簧的弹力随着弹簧压缩量减小而变小,开始时,小球受到弹簧的弹力大于小球的重力,速度增大,当弹簧的弹力小于小球的重力时,速度减小,故小球的速度先增大后减小,B错误;开始时,\( F_{\text{弹}}>mg \),\( F_{\text{弹}} – mg = ma \),\( F_{\text{弹}} \downarrow \to a \downarrow \),当\( F_{\text{弹}}<mg \)时,\( mg – F_{\text{弹}} = ma \),\( F_{\text{弹}} \downarrow \to a \uparrow \),所以小球的加速度先减小后增大,C错误;小球与弹簧组成的系统机械能守恒,因小球的速度先增大后减小,故其动能先增大后减小,则小球与弹簧组成的系统重力势能与弹性势能之和先减小后增大,D正确。
(2024届广东部分高中二模)(多选)人们有时用“打夯”的方式把松散的地面夯实。设某次打夯符合以下模型:如图所示,两人同时通过绳子对质量为\( m \)的重物分别施加大小均为\( mg \)(\( g \)为重力加速度的大小)、方向都与竖直方向保持\( 37^{\circ} \)角的力,重物离开地面\( h \)高度后人停止施力,最后重物自由下落砸入地面的深度为\( \frac{h}{10} \)。\( \cos 37^{\circ}=0.8 \),不计空气阻力,则()
A.重物在空中上升的时间一定大于在空中下落的时间
B.重物克服地面阻力做的功等于人对重物做的功
C.重物刚落地时的速度大小为\( \sqrt{2gh} \)
D.地面对重物的平均阻力大小为\( 17mg \)
展开答案
【答案】AD
【解析】设停止施力瞬间重物的速度大小为\( v_1 \),根据动能定理有\( (2F \cos 37^{\circ}-mg)h = \frac{1}{2}mv_1^2 \),又\( F = mg \),解得\( v_1 = \sqrt{1.2gh} \)。设重物刚落地时的速度大小为\( v_2 \),从开始施力到重物落地瞬间的过程,根据动能定理有\( 2F \cos 37^{\circ} \cdot h = \frac{1}{2}mv_2^2 \),解得\( v_2 = \sqrt{3.2gh} \),C错误。
重物在空中运动过程,先在拉力作用下向上做匀加速运动,速度大小达到\( v_1 \)后向上做匀减速运动直至速度为零,之后再向下做匀加速直线运动直至速度大小为\( v_2 \)。可知上升过程中的平均速度大小为\( \bar{v_1} = \frac{v_1}{2} \),在空中下落过程中的平均速度大小为\( \bar{v_2} = \frac{v_2}{2} \)。上升过程、在空中下落过程的位移大小相等,则重物在空中上升的时间一定大于在空中下落的时间,A正确。
重物在整个运动过程中,根据动能定理有\( W_{\text{人}} + W_G – W_{\text{阻}} = 0 \),又\( W_G = mg \frac{h}{10} > 0 \),则重物克服地面阻力做的功大于人对重物做的功,B错误。 根据动能定理有\( 2F \cos 37^{\circ} \cdot h + mg \frac{h}{10} – F_{\text{阻}} \frac{h}{10} = 0 \),解得地面对重物的平均阻力大小\( F_{\text{阻}} = 17mg \),D正确。
