理想气体经典计算题
如图所示,活塞质量为m=0.1 kg、横截面积为S=1.0 cm²,导热良好、质量M=0.2 kg的气缸通过弹簧吊在空中,弹簧的劲度系数为k=300N/m,气缸内封闭一定质量的空气,气缸内壁与活塞间无摩擦不漏气,初态气缸底部距地面h=1.0cm,活塞到气缸底部的距离为L=27 cm,大气压强为p0=1.0×10 Pa,环境温度为t1=-3℃,重力加速度g取10m/s²,热力学温度与摄氏温度的关系为T=(t+273)K.
(1)求初态被封闭气体的压强p1;
(2)若环境温度缓缓升高到T2时,气缸底部刚好接触地面且无挤压,求T2;
(3)若环境温度继续升高到T时,弹簧恰好恢复原长,求T3.
展开答案
(1)初态气体压强计算(共4分)
以汽缸为研究对象受力分析,由平衡条件得:
$$ p_0 S = p_1 S + Mg \tag{2分} $$
解得:
$$ p_1 = \boxed{8\times10^4\ \text{Pa}} \tag{2分} $$
(2)温度$T_2$计算(共4分)
系统平衡条件:
$$ F = (M + m)g = (0.2+0.1)\times10 = \boxed{3\ \text{N}} \tag{1分} $$
胡克定律:
$$ x = \frac{F}{k} = \frac{3}{300} = \boxed{1\ \text{cm}} \tag{1分} $$
盖-吕萨克定律:
$$ \frac{L_1}{T_1} = \frac{L_2}{T_2} \quad (L_1=27\ \text{cm},\ T_1=270\ \text{K},\ L_2=28\ \text{cm}) \tag{1分} $$
解得:
$$ T_2 = 270\times\frac{28}{27} = \boxed{280\ \text{K}}\ (\text{7℃}) \tag{1分} $$
(3)温度$T_3$计算(共4分)
压强平衡条件:
$$ p_1 S = p_3 S \Rightarrow p_3 = \boxed{1.1\times10^5\ \text{Pa}} \tag{1分} $$
气柱长度:
$$ L_3 = L_1 + h + x = 27 + 1 + 1 = \boxed{29\ \text{cm}} \tag{1分} $$
理想气体方程:
$$ \frac{p_1 L_1}{T_1} = \frac{p_3 L_3}{T_3} \tag{2分} $$
解得:
$$ T_3 = \boxed{398.75\ \text{K}}\ (\text{125.75℃}) \tag{1分} $$
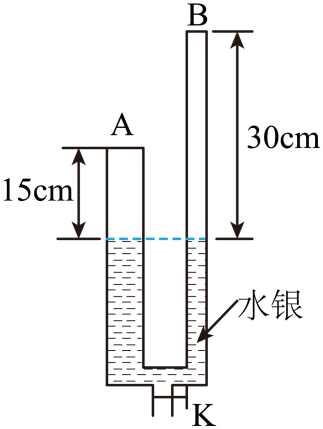
如图,顶部封闭竖直放置的不对称U形玻璃管中,左侧A管的横截面积是右侧B管的2倍,管中充有水银,A管和B管中水银液面的高度相同,水银液面上方的管中有压强均为84cmHg的空气,A管中空气柱的长度为15cm,B管中空气柱的长度为30cm。打开管底部的阀门K,缓慢放出部分水银后再关闭
K。已知放出部分水银后B管中水银面下降了5cm,在放出水银的过程中温度保持不变。求A管中水银面下降的高度。
展开答案
【答案】3cm
【详解】B管内气体做等温变化,则
$$ p_{B0}Sh_{B} = p_{B}S(h_{B} + \Delta h_{B}) $$
其中
$$ p_{B0} = 84\,\text{cmHg},\quad h_{B} = 30\,\text{cm},\quad \Delta h_{B} = 5\,\text{cm} $$
解得
$$ p_{B} = 72\,\text{cmHg} $$
A管内气体做等温变化,则
$$ p_{A0} \cdot 2Sh_{B} = p_{A} \cdot 2S(h_{A} + \Delta h_{A}) $$
其中
$$ p_{A0} = 84\,\text{cmHg},\quad h_{A} = 15\,\text{cm} $$
装置稳定后有
$$ p_{A} + \rho g(\Delta h_{B} – \Delta h_{A}) = p_{B} $$
联立解得
$$ p_{A} = 70\,\text{cmHg},\quad \Delta h_{A} = 3\,\text{cm} $$
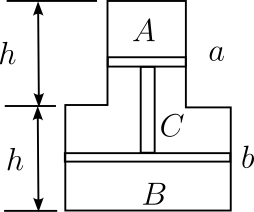
如图所示,”凸”形汽缸上、下部分高度均为$h$,上、下底面导热良好,其余部分绝热。上部分横截面积为$S$,下部分横截面积为$2S$。
汽缸被总重力$G = 2p_0S$、中间用轻杆相连的$a$、$b$两绝热活塞(密封性良好)分成$A$、$B$、$C$三部分,活塞稳定时$A$、$B$、$C$三个部分内的气体温度均为$T$,$A$、$C$部分气体压强为$p_0$,$A$、$B$部分高均为$\frac{h}{2}$,$C$部分高为$h$。
现保持$A$、$B$温度不变,使$C$中的气体温度缓慢变化至某温度,最终稳定后两活塞缓慢下降了$\frac{h}{4}$,不计所有摩擦。求:
- $C$温度变化前,$B$中气体的压强;
- $C$中气体最终温度为多少?
展开答案
【解析】
[(1)] $C$温度变化前,对两活塞列平衡方程:
$$2p_{0}S + p_{0}S + p_{0}\cdot 2S = p_{B}\cdot 2S + p_{0}S$$
解得:
$$p_{B} = 2p_{0}$$
[(2)] $A$中气体状态分析:
初状态:
$$p_{A1}=p_{0},\quad V_{A1}=S\frac{h}{2},\quad T_{A1}=T$$
末状态:
$$V_{A2}=S\left(\frac{h}{2}+\frac{h}{4}\right),\quad T_{A2}=T$$
由玻意耳定律:
$$p_{A1}V_{A1} = p_{A2}V_{A2}$$
解得:
$$p_{A2} = \frac{2}{3}p_{0}$$
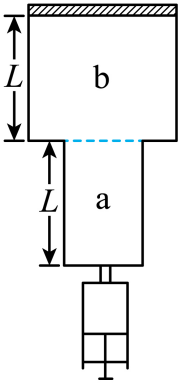
如图所示,竖直放置的卡腰式圆柱形气缸由$a$、$b$两部分组成,两部分高度均为$L=10\,\text{cm}$,气缸$a$的横截面积$S=20\,\text{cm}^2$,气缸$b$的横截面积是$a$的2倍,气缸$a$的下端装有抽气筒。气缸$b$中有光滑活塞(厚度不计),活塞质量为$m=20\,\text{kg}$,活塞与气缸间封闭性良好。初始状态活塞恰好在气缸$b$的上端,现对气缸进行缓慢抽气,共抽气22次,每次抽出气体的体积均为$V_{0}=20\,\text{mL}$。温度保持不变,大气压强为$P_{0}=1.0\times10^{5}\,\text{Pa}$。求:
(1)前10次抽气过程中气缸$b$中的活塞对气体做的功;
(2)整个抽气过程结束后,气缸内气体的压强;
(3)整个抽气过程结束后,抽出气体的质量占抽气前气体质量的百分比。
展开答案
【答案】(1)30J;(2)1.24×105Pa;(3)72.4%
【详解】(1)由题意可知气缸b的横截面积为
$S_b=40cm^2$
气缸b的容积为
$V_b=400cm^3$
气缸内气体的压强为:
$$p = p_0 + \frac{mg}{S_b} = 1.5 \times 10^5 \,\text{Pa}$$
前10次抽气过程中抽出气体的体积为:
$$\Delta V = 10V_0 = 200\,\text{ml} = 200\,\text{cm}^3$$
(因$\Delta V$小于气缸$b$的容积)前10次抽气过程均为等压变化,活塞对气体做功:
$$W = p\Delta V = 1.5 \times 10^5 \times 200 \times 10^{-6} \,\text{J} = 30\,\text{J}$$
气缸$a$的容积:
$$V_a = 200\,\text{cm}^3$$
抽气20次后活塞恰达到卡腰处,气缸内压强:
$$p = 1.5 \times 10^5 \,\text{Pa}$$
第21次抽气过程(玻意耳定律):
$$pV_a = p_{21}(V_a + V_0)$$
解得:
$$p_{21} = \frac{10}{11}p$$
第22次抽气过程同理:
$$p_{21}V_a = p_{22}(V_a + V_0)$$
由理想气体状态方程得:
$$p_{21}V_{\mathrm{a}} = p_{22}(V_{\mathrm{a}}+V_{0})$$
解得:
$$p_{22} = \left(\frac{10}{11}\right)^{2}p = 1.24 \times 10^{5}\,\text{Pa}$$
(3)由理想气体密度方程得:
$$\frac{p}{\rho} = \frac{p_{22}}{\rho_{22}}$$
整个抽气过程结束后剩余气体的质量与抽气前气体质量比为:
$$\frac{m_{22}}{m} = \frac{\rho_{22}V_{\mathrm{a}}}{\rho(V_{\mathrm{a}}+V_{\mathrm{b}})}$$
故整个抽气过程结束后,抽出气体的质量占抽气前气体质量的百分比为:
$$\frac{m – m_{22}}{m} \times 100\% = 72.4\%$$
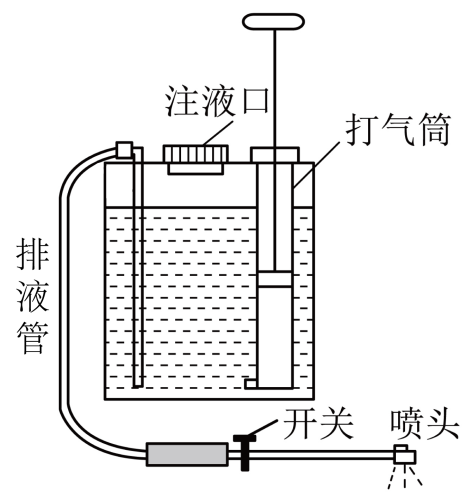
如图,是常用的一种便携式喷雾器的原理图,其储液罐总容积为$V$。现装入$0.8V$的药液后并盖好注液口密封盖,然后通过打气筒向罐中打气,每次均能把$\frac{1}{25}V$的外界空气打进罐中。设打气过程中气体的温度没有变化,忽略排液管中的液体体积及罐中排液管液柱产生的压强,已知外界大气压强为$p_0$,密封气体可视为理想气体。则:
\begin{enumerate}
\item[(1)] 不喷药液时,要使储液罐中的气体压强达到$4p_0$,则打气筒打气的次数是多少?
展开答案
【答案】(1)15次;(2)20次
【详解】
状态参数设定:
• 初态: $$ p_1 = p_0 $$
$$ V_1 = 0.2V + N \cdot \frac{1}{25}V $$
• 末态: $$ p_2 = 4p_0 $$
$$ V_2 = 0.2V $$应用玻意耳定律(等温过程):
$$ p_1V_1 = p_2V_2 $$
$$ p_0 \left(0.2V + \frac{N}{25}V \right) = 4p_0 \cdot 0.2V $$方程求解:
$$ 0.2 + \frac{N}{25} = 0.8 $$
$$ \frac{N}{25} = 0.6 $$
$$ N = 15 $$
设打气次数为$N$,对压强为$4p_0$的罐中气体:
初态参数:
$$ p_1 = p_0 $$
$$ V_1 = 0.2V + N \cdot \frac{1}{25}V $$
末态参数:
$$ p_2 = 4p_0 $$
$$ V_2 = 0.2V $$
由玻意耳定律(等温变化):
$$ p_1V_1 = p_2V_2 $$
代入数据得:
$$ p_0(0.2V + \frac{N}{25}V) = 4p_0 \cdot 0.2V $$
解得:
$$ N = 20 $$
如图,一容器由横截面积分别为2S和S的两个汽缸连通而成,容器平放在水平地面上,汽缸内壁光滑。整个容器被通过刚性杆连接的两活塞分隔成三部分,分别充有氢气、空气和氮气。平衡时,氮气的压强和体积分别为p0和V0,氢气的体积为2V0,空气的压强为p,现缓慢地将中部的空气全部抽出,抽气过程中氢气和氮气的温度保持不变,活塞没有到达两汽缸的连接处,求:
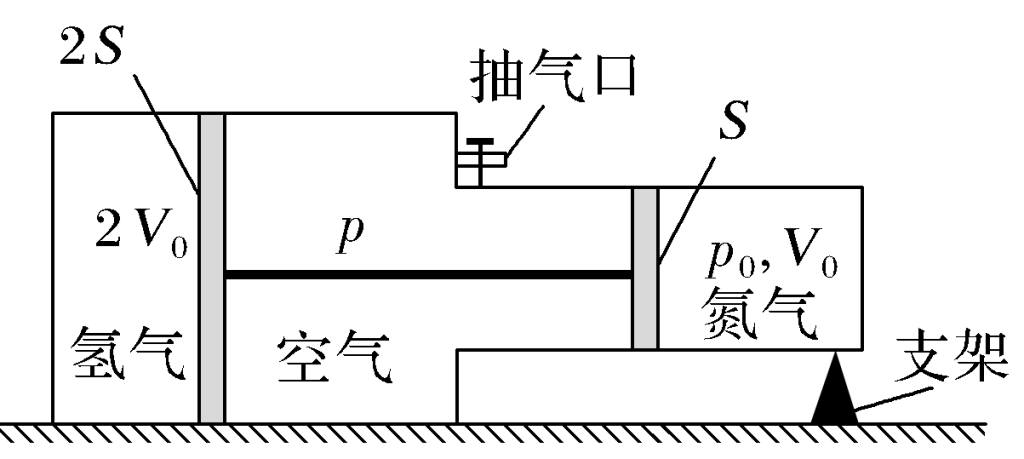
(ⅰ)抽气前氢气的压强;
(ⅱ)抽气后氢气的压强和体积。
【答案】
(ⅰ)$\dfrac{1}{2}(p_0+p)$ (ⅱ)$\dfrac{1}{2}p_0+\dfrac{1}{4}p$ $V_1=\dfrac{4(p_0+p)V_0}{2P_)+P}$
【解析】 (ⅰ)设抽气前氢气的压强为p10,根据力的平衡条件得
(p10-p)·2S=(p0-p)S①
得$p_{10}\dfrac{1}{2}(p_0+p)$②
(ⅱ)设抽气后氢气的压强和体积分别为p1和$(2V_0-2S\Delta x$,氮气的压强和体积分别为p2和$V_0- S\Delta x$。根据力的平衡条件有
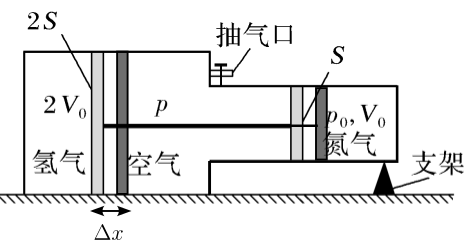
$p_2S=p_1·2S$③
由玻意耳定律得$p_1(2V_0-2S\Delta x)=p_{10}·2V_0$④
$p_2(V_0- S\Delta x)$p2V2=p0V0⑤
由于两活塞用刚性杆连接,故
联立②③④⑤式解得
$p_1=\dfrac{1}{2}p_0+\dfrac{1}{4}p$⑦
$V_1=\dfrac{4(p_0+p)V_0}{2P_0+P}$⑧
