动量冲量计算题训练
激光由于其单色性好、亮度高、方向性好等特点,在科技前沿的许多领域有着广泛的应用。根据光的波粒二象性可知,当光与其他物体发生相互作用时,光子表现出有能量和动量,对于波长为λ的光子,其动量$p=\dfrac{h}{\lambda}$。已知光在真空中的传播速度为$c$,普朗克常量为$h$。
(1)科研人员曾用强激光做过一个有趣的实验:一个水平放置的小玻璃片被一束强激光托在空中。已知激光竖直向上照射到质量为m的小玻璃片上后,全部被小玻璃片吸收,重力加速度为g。求激光照射到小玻璃片上的功率P;
(2)激光冷却和原子捕获技术在科学上意义重大,特别是对生物科学将产生重大影响。所谓激光冷却就是在激光的作用下使得做热运动的原子减速,其具体过程如下:一质量为m的原子沿着x轴负方向运动,频率为$v_0$的激光束迎面射向该原子。运动着的原子就会吸收迎面而来的光子从基态跃迁,而处于激发态的原子会立即自发地辐射光子回到基态。原子自发辐射的光子方向是随机的,在上述过程中原子的速率已经很小,因而光子向各方向辐射光子的可能性可认为是均等的,因而辐射不再对原子产生合外力的作用效果,并且原子的质量没有变化。
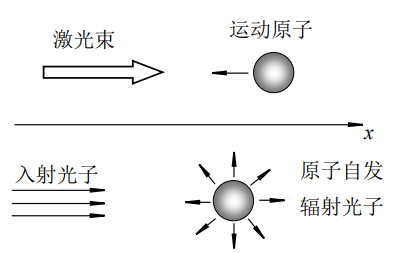
- ①设原子单位时间内与$n$个光子发生相互作用,求运动原子做减速运动的加速度$a$的大小;
- ②假设某原子以速度$v_0$沿着x轴负方向运动,当该原子发生共振吸收后跃迁到了第一激发态,吸收一个光子后原子的速度大小发生变化,方向未变。求该原子的第一激发态和基态的能级差ΔE?
展开答案
【答案】(1)$p=mgc$ ;(2) ①$a=\dfrac{nhv_0}{cm}$;②$\Delta E =hv_0(1+\dfrac{v_0}{c})-\dfrac{h^2v_0^2}{2c^2m}$
【详解】
(1)设在∆t时间内照射到玻璃表面的光子数为n,则由动量定理
$F\Delta t=np$
对玻璃板由平衡知识
$F=mg$
每个光子的能量
$E=hv=\dfrac{hc}{\lambda}=cp$
激光照射到小玻璃片上的功率
$P=\dfrac{nE}{\Delta t}$
解得
$P=mgc$
(2)①原子单位时间内与n个光子发生相互作用,由动量守恒定律
$n\dfrac{hv_0}{c}=m\Delta v$
原子的加速度
$a=\dfrac{\Delta v}{\Delta t}$
其中∆t=1s解得
$a=\dfrac{nhv_0}{cm}$
②以原子开始运动的方向为正方向,原子吸收一个光子的过程,由动量守恒定律
$mv_0-\dfrac{hv_0}{c}=mv$
该原子的第一激发态和基态的能级差
$\Delta = \dfrac{1}{2}mv_0^2+hv_0-\dfrac{1}{2}mv^2$
解得
$\Delta E = hv_0(1+\dfrac{v_0}{c})-\dfrac{h^2v_0^2}{2c^2m}$
质量为M=4kg的长木板A静止放在光滑水平地面上,质量为m1=4kg的小物块B位于木板A的左端,质量为m2=4kg的物块C位于木板A的右端,物块B与木板A间的动摩擦因数为μ=0.5,C物块下表面光滑。某时刻,使物块B以速度v1=2m/s的速度从左到右运动,同时使物块C以速度v2=2m/s从右向左运动,已知当A、B速度相等时,B、C发生碰撞,碰后粘在一起运动,重力加速度g取10m/s2,B、C均看为质点,则:
(1)木板A的最大速度为多少?
(2)A、B间摩擦产生的热量为多少?
展开答案
【解析】
(1)B、C碰撞前,A做加速运动,B、C碰撞后,A做减速运动,故A、B速度相等时,A的速度最大;
对A、B系统,取向右为正方向,由动量守恒定律:$m_1v_1=(m_1+M)v$
解得$v=1m/s$
(2)B、C碰撞过程,取向右为正方向,由动量守恒定律得:$m_1v-m_2v_2=(m_1+m_2)v′$
解得:$v′=-0.5m/s$
碰撞过程中能量损失为:$\Delta E_1=\dfrac{1}{2}m_1v^2+\dfrac{1}{2}m_2v_2^2-\dfrac{1}{2}(m_1+m_2)v′^2$
解得:$\Delta E_1$=9J
当A、B、C相对静止时有:$m_1v_1-m_2v_2=(M+m_1+m_2)v″$
解得:$v″=0$
A、B间摩擦产生的热量:$Q=\dfrac{1}{2}m_1v_2^2+\dfrac{1}{2}m_2v_2^2-\Delta E_1$
解得:Q=7J。
真空中存在电场强度大小为E1的匀强电场,一带电油滴在该电场中竖直向上做匀速直线运动,速度大小为v0,在油滴处于位置A时,将电场强度的大小突然增大到某值,但保持其方向不变.持续一段时间t1后,又突然将电场反向,但保持其大小不变;再持续同样一段时间后,油滴运动到B点.重力加速度大小为g.
(1)油滴运动到B点时的速度;
(2)求增大后的电场强度的大小;为保证后来的电场强度比原来的大,试给出相应的t1和v0应满足的条件.已知不存在电场时,油滴以初速度v0做竖直上抛运动的最大高度恰好等于B、A两点间距离的两倍.
展开答案
【分析】
(1)分析油滴的运动过程,可知其先进行向上的匀速直线运动,到达A处后因电场强度突然增大而开始做向上的匀加速直线运动,经过t1后电场突然反向,油滴开始做匀减速直线运动,并可能在速度减为零后做反向的匀加速直线运动.对电场增大后的两个过程分别列出牛顿第二定律方程,即可求得两个过程中的加速度,而t1又是一个已知量,那么直接使用运动学公式即可求出vB的速度大小;
(2)因为油滴最后可能做反向的匀加速直线运动,因此我们不能确定B点的位置究竟在A点上方还是A点下方,故需要分为两种情况讨论.对其中每一种情况,根据运动学公式列出方程,并与竖直上抛的方程进行联立,即可分别求得两种情况下的场强E2的大小;而根据题意,为求出t1与v0满足的条件,只需要使E2>E1即可,那么就可以最终求得t1与v0间的关系式.
【解答】 解:(1)设油滴质量为m,带电荷量为q,增大后的电场强度为$E_2$,根据题中条件可以判断电场力与重力方向相反;
对于匀速运动阶段,有$qE_1=mg$…①
对于场强突然增大后的第一段$t_1$时间,由牛顿第二定律得:$qE_2-mg=ma_1$…②
对于场强第二段$t_1$时间,由牛顿第二定律得:$qE_2+mg=ma_2$ …③
由运动学公式,可得油滴在电场反向时的速度为:$v_1=v_0+a_1t_1$④
油滴在B的速度为:$v_B=v_1-a_2t_1$…⑤
联立①至⑤式,可得:$v_B=v_0-2gt_1$;方向向上;
方法二:还记得冲量是改变速度的原因吧?上下时间相等,而增加部分的电场力是一样的,所以向上的冲量和向下的冲量是一样的,所以不会影响速度变化,所以vB=v0-2gt1。(2)设无电场时竖直上抛的最大高度为h,由运动学公式,有:${v_0}^2=2gh$…⑥
根据位移时间关系可得:$v_0t_1+\frac{1}{2}a_1{t_1}^2=x1$…⑦
$v_1t_1-\frac{1}{2}a_2{t_1}^2=x2$…⑧
油滴运动有两种情况:
情况一:
位移之和$x_1+x_2=\frac{h}{2}$ ⑨
联立①、②、③、⑥、⑦、⑧、⑨可得:
$E_2=E_1+\frac{E_1}{g} (g+\frac{v^2}{4g{t_1}^2}−\frac{2v_0}{t_1}) $
由题意得$E_2>E_1$由题意满足条件$\frac{2v_0}{t_1}−\frac{{v_0}^2}{4{t_1}^2}<g$
即当$0<t_1<(1−\frac{\sqrt{3}}{2})\frac{v_0}{g}$或$t_1>(1+\frac{\sqrt{3}}{2})\frac{v_0}{g}$才是可能的;
情况二:
位移之和$x_1+x_2=-\frac{h}{2}$⑩
联立①、②、③、⑥、⑦、⑧、⑩可得:
$E_2=E_1+\frac{E_1}{g} (g-\frac{v^2}{4g{t_1}^2}−\frac{2v_0}{t_1}) $
由题意得$E_2>E_1$,即满足条件$\frac{2v_0}{t_1}+\frac{{v_0}^2}{4{t_1}^2}<g $,即$t_1>(1+\frac{\sqrt{5}}{2})\frac{v_0}{g}$,另一解为负,不合题意,舍去.
答:
(1)油滴运动到B点时的速度为:$v_B=v_0-2gt_1$;
(2)增大后的电场强度的大小为$E_1+\frac{E_1}{g}(g+\frac{{v_0}^2}{{t_1}^2}−\frac{2v_0}{t_1})$,t1和v0应满足的条件为$0<t_1<(1−\frac{\sqrt{3}}{2})\frac{v_0}{g}$或$t_1>(1+\frac{\sqrt{3}}{2})\frac{v_0}{g}$
或$E_1+\frac{E_1}{g} (g-\frac{v^2}{4g{t_1}^2}−\frac{2v_0}{t_1}) $;相应的t1和v0应满足的条件为$t_1>(1+\frac{\sqrt{5}}{2})\frac{v_0}{g}$
如图所示,甲车质量\(m_{1} = 20\ \text{kg}\),车上有质量\(M = 50\ \text{kg}\)的人,甲车(连同车上的人)以\(v = 3\ \text{m/s}\)的速度向右滑行,此时质量\(m_{2} = 50\ \text{kg}\)的乙车正以\(v_{0}=1.8\ \text{m/s}\)的速度迎面滑来,为了避免两车相撞,当两车相距适当距离时,人从甲车跳到乙车上,求人跳出甲车的水平速度(相对地面)应当在什么范围内才能避免两车相撞。(不计地面和小车的摩擦,且乙车足够长)
展开答案
解 1. 两车恰好不相撞的临界情况是:人跳到乙车后,两车速度相同。设共同速度为\(v’\)。
2. 对甲、乙车和人组成的系统应用动量守恒定律
规定向右为正方向,系统总动量守恒,初始总动量\(p=(m_{1}+M)v – m_{2}v_{0}\)。 – 末态总动量\(p’=(m_{1}+m_{2}+M)v’\)。
– 根据动量守恒定律即\((m_{1}+M)v – m_{2}v_{0}=(m_{1}+m_{2}+M)v’\)。
– 代入数据\(m_{1} = 20\ \text{kg}\),\(M = 50\ \text{kg}\),\(v = 3\ \text{m/s}\),\(m_{2} = 50\ \text{kg}\),\(v_{0}=1.8\ \text{m/s}\):
– 左边\((20 + 50)\times3-50\times1.8=70\times3 – 90 = 210 – 90=120\)。
– 右边\((20 + 50+50)v’ = 120v’\)。
– 由\(120 = 120v’\),解得\(v’ = 1\ \text{m/s}\)。
3. 对人跳离甲车过程应用动量守恒定律
– 设人跳出甲车的速度为\(u\),对人跳离甲车过程,以向右为正方向,根据动量守恒定律\((m_{1}+M)v = m_{1}v’+Mu\)。
变形可得\(u=\frac{(m_{1}+M)v – m_{1}v’}{M}\)。
把\(m_{1} = 20\ \text{kg}\),\(M = 50\ \text{kg}\),\(v = 3\ \text{m/s}\),\(v’ = 1\ \text{m/s}\)代入:
\(u=\frac{(20 + 50)\times3-20\times1}{50}=\frac{210 – 20}{50}=\frac{190}{50}=3.8\ \text{m/s}\)。
所以,人跳出甲车的水平速度\(u\geqslant3.8\ \text{m/s}\)时,才能避免两车相撞。
5如图所示,一质量为 \( M = 2\ \text{kg} \)、右端带有一段半径为 \( R = 0.5\ \text{m} \) 的四分之一圆弧的长木板停靠在墙边,木板左端固定一轻弹簧,弹簧右端紧靠一质量为 \( m = 1\ \text{kg} \) 的小物块(不拴接),木板表面除长为 \( L = 2.5\ \text{m} \) 的 \( AB \) 段外均光滑,\( AB \) 段与物块间的动摩擦因数 \( \mu = 0.2 \)。现用外力通过物块压缩弹簧,使其弹性势能 \( E_{\text{p}} = 18\ \text{J} \),然后由静止释放物块。已知物块到达 \( A \) 点前已脱离弹簧,水平地面光滑且足够长,重力加速度 \( g \) 取 \( 10\ \text{m/s}^2 \)。
(1) 求物块第一次到达 \( A \) 点时的动量大小;
(2) 试通过计算判断物块能否到达圆弧轨道的最高点。
求: (1)若\(n = 2\),引爆炸药时,滑块B的初速度大小\(v_{1}\)。
(2)若\(n = 2\),且小车C固定不动,则滑块A和B分别相对小车C运动的路程之比;
(3)若\(1\leq n\leq5\),小车C不固定,则滑块A和B相对小车C静止时,它们之间的距离x的范围。
展开答案
解析 (1)由能量守恒定律得\( E_{\text{p}} = \frac{1}{2}mv_{0}^{2} \), 解得\( v_{0} = 6\ \text{m/s} \), 物块第一次到达A点时的动量大小\( p = mv_{0} = 6\ \text{kg·m/s} \)。
(2)设物块脱离弹簧后第一次与木板在水平方向共速时的速度大小为\( v \),物块与木板组成的系统水平方向动量守恒,由动量守恒定律有\( mv_{0} = (M + m)v \), 可得\( v = 2\ \text{m/s} \), 设此时物块上升的高度为\( h \), 由功能关系得\( \frac{1}{2}mv_{0}^{2} – \mu mgL = \frac{1}{2}(M + m)v^{2} + mgh \), 可得\( h = 0.7\ \text{m} > R = 0.5\ \text{m} \),故物块能到达圆弧轨道最高点。
如图所示,滑块A和B质量分别为m和nm,静止在小车C上,与小车C之间的动摩擦因数均为μ,且nμ = 0.4。小车C静止在光滑的水平面上,质量为nm。在下述情境中,通过点燃夹在滑块A和B之间的适量炸药,使滑块A获得向左的初速度\(v_{0}=1.2m/s\)。滑块A和B始终没有脱离小车C。重力加速度g取\(10m/s^{2}\)。
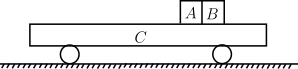
求: (1)若\(n = 2\),引爆炸药时,滑块B的初速度大小\(v_{1}\)。
(2)若\(n = 2\),且小车C固定不动,则滑块A和B分别相对小车C运动的路程之比;
(3)若\(1\leq n\leq5\),小车C不固定,则滑块A和B相对小车C静止时,它们之间的距离x的范围。
展开答案
【解析】(1)点燃炸药,\(A\)、\(B\)组成的系统动量守恒,有\(mv_{0}=nmv_{1}\), 若\(n = 2\),则\(v_{1}=\frac{v_{0}}{2}=0.6m/s\)。
(2)爆炸后,对滑块\(A\)由牛顿第二定律有\(\mu mg = ma\), 滑块\(A\)和滑块\(B\)在小车上滑动时的加速度大小均为 \(a = \mu g = 2m/s^{2}\), 设滑块\(A\)和\(B\)分别相对小车\(C\)运动的路程为\(x\)和\(x’\), 由运动学公式有\(v_{0}^{2}=2ax\),\(v_{1}^{2}=2ax’\), 代入数据得\(\frac{x}{x’}=4\)。
(3)取水平向右为正方向,设小车的加速度大小为\(a_{1}\),\(B\)的加速度大小为\(a_{2}\),由牛顿第二定律可得\(\mu nmg – \mu mg = nma_{1}\), 解得\(a_{1}=\frac{n – 1}{n}\mu g\),
当\(1\leq n\leq5\)时,\(a_{1}>0\),故小车向右加速,设经\(t_{1}\)时间滑块\(B\)和小车\(C\)达到共同速度\(v_{2}\), 对\(C\),有\(v_{2}=a_{1}t_{1}\),对\(B\),有\(v_{2}=v_{1}-at_{1}\), \(B\)、\(C\)共速后一起匀减速,滑块\(A\)、\(B\)和小车\(C\)所受合外力为\(0\),系统动量守恒,故最终三者同时静止,设滑块\(A\)运动时间为\(t_{2}\),则
\(0 = v_{0}-at_{2}\), 设滑块\(A\)和\(B\)分别相对小车\(C\)运动的距离为\(x_{1}\)和\(x_{2}\),
则\(x_{1}=\frac{v_{2}}{2}t_{2}+\frac{v_{0}}{2}t_{2}\),\(x_{2}=\frac{v_{1}+v_{2}}{2}t_{1}-\frac{v_{2}}{2}t_{1}\),滑块\(A\)、\(B\)之间的距离为\(x = x_{1}+x_{2}\),
联立得\(x = \frac{0.36n^{2}}{2n – 1}m=\frac{0.36}{1-(1 – \frac{1}{n})^{2}}m\),可知\(n\)越大,\(x\)越大, 将\(1\leq n\leq5\)代入得\(0.36m\leq x\leq1m\)。
